Issue, No.2 (June 2017)
The Active Ingredient of Inequality1
Most users of LIS data and readers of a newsletter entitled “Inequality Matters” probably need not be convinced that inequality is important. But which inequality do we care most about? Or, to paraphrase the title of Amartya Sen’s famous 1979 Tanner Lecture, “inequality of what?” (Sen, 1980).
The question can be rephrased as follows: in an ideal, just world, what is it that ought to be (perfectly) equally distributed? I suspect that very few people would answer “income” or “wealth” to such a question. Of course, many of us might prefer incomes and wealth to be distributed less unequally than they currently are. But would people generally claim that a fair society is one in which everyone has exactly the same level of income, or wealth?
Political philosophers and economists, from John Rawls and Amartya Sen to Richard Arneson and John Roemer, have argued that income and wealth are not the appropriate “equalizandum” in the pursuit of a fair society. Rather, they see a just society as one in which people have the same life chances, the same basic set of opportunities to flourish. Terminology and conceptual nuances vary: Sen’s capabilities are not the same as Ronald Dworkin’s resources, which are not the same as Arneson’s or Roemer’s opportunities. But broadly speaking, these scholars have argued that it is people’s choice sets – their opportunities – that should be equalized.
Outcome differences that truly arise from the exercise of personal choices, given identical choice sets, might be ethically acceptable. But those that arise from differences in circumstances over which individuals have no control, and which shape choice sets (such as family background, race, gender, place of birth, or whether you happen to enter the labor market during a recession) are not. It is this latter kind of inequality that we call inequality of opportunity (IOp), and truly object to.
Fine. But can inequality of opportunity be measured and quantified?
The trouble, of course, is that “opportunities” are, by definition, mostly unobserved counterfactuals. The one choice you end up making may be observed, but the choice set from which you made it is typically not. For a long time, this made quantifying inequality of opportunity rather difficult. There is a literature on comparing distributions of opportunity sets that attempts to approach this question directly but, although it is conceptually very elegant, it has yielded limited or no progress on the empirical front; see Barberà et al. (2004) for a survey.
More recently, progress was made through the adoption of a more indirect approach: if equality of opportunity requires that pre-determined circumstances (beyond the control of the individual) have no effect on outcomes, then over large populations and under equality of opportunity, outcomes should be distributed independently of those circumstances. And if that is so, then perhaps we can measure inequality of opportunity by assessing the extent to which that condition is violated in actual data for the joint distribution of outcomes (say, income) and circumstances (say, race and parental background).
The general approach, as Vito Peragine and I have described it, is to express the distribution of the outcome of interest (say, income) as a matrix, where the rows correspond to groups with identical circumstances (often referred to as ‘types’), and the columns correspond to groups that exert identical degrees of effort, or personal responsibility2. In principle, if one could eliminate from such a matrix all (and only) the ‘fair’ inequality – that is, outcome differences due to personal effort or responsibility – then the inequality left over would be inequality of opportunity. One could just apply one’s favorite inequality measure to this counterfactual matrix, and obtain a measure of IOp.
This has been done, and it has been done in a number of different ways; see Ferreira and Peragine (2016) for a discussion. One particular method that is conceptually simple, and has been applied fairly widely, is to consider any inequality among people sharing the same exact circumstances (say, women aged 30-35, who have immigrated to France from North Africa, born from parents with no more than high-school education) as ‘fair’. One could then replace the entries along each row of our matrix (i.e. within each type) with some relevant constant (say, the row mean), and compute inequality in the resulting, counterfactual matrix. This would yield a well-defined measure of inequality between types, which has been interpreted as a lower-bound for inequality of opportunity in a number of papers.
As a share of total inequality, these measures of inequality of opportunity can be quite substantial. Using household consumption expenditure as the outcome variable, one study for five Latin American countries found IOp to range from 25% of overall mean log deviation (in Colombia) to 51% in Guatemala (Ferreira and Gignoux 2011). Shares for Ecuador, Panama and Peru ranged from 33% to 38%. And that was using a rather sparse set of circumstance variables: gender, ethnicity, father’s and mother’s education, father’s and mother’s occupation, and region of birth, yielding at most 108 types per country. One can easily imagine that a finer partition of society into types, drawing on richer information about other circumstances, such as parental income; parental behaviors during pregnancy and early childhood, exogenous shocks during schooling, and so on, would yield even larger measures of IOp as a share of inequality of opportunity.
But can it be well measured?
Therein, of course, lies a problem. Researchers never observe a complete set of circumstance variables: all the different factors that might influence the outcome of interest, but are exogenous to (in the sense of taken as given, rather than chosen, by) the individual. The list of observed circumstances is always incomplete, and the measure of between-types IOp is therefore always a lower-bound. Pointing to this weakness, this approach has been criticized for yielding numbers that are too low, and may mislead policy-makers into a false sense of complacency that “most inequality is fair”.
Can we do better? Can IOp be measured more accurately than in the early “between-types” papers? Two recent approaches seem to me particularly promising. One departs from the conservative early practice of using only variables determined prior to or at birth as circumstances, and enlarges the set by treating a range of childhood variables, up to a certain “age of consent” (such as ability test scores, indicators of the quality of parent-child relationship, etc.), as lying outside the child’s responsibility. Using this approach on variable-rich datasets such as the British Cohort Study for the UK and the National Longitudinal Survey of Youth for the US, Hufe et al. (2015) find that IOp can account for as much as 31% of total inequality in the UK, and 45% in the US. Previous estimates for both countries were in the 18-20% range.
The second approach uses panel data to estimate an upper-bound for IOp, to complement the lower-bound measures described earlier. The basic idea is to treat circumstances as time-invariant, and to use individual fixed-effects to put a ceiling on the share of inequality that they could explain. Niehues and Peichl (2014) find upper-bound estimates for inequality of opportunity for permanent net earnings in Germany and the US of 60% of total inequality, or more.
While these two approaches illustrate promising ways forward in improving the accuracy – and thus the policy relevance – of IOp measurement, they also highlight how crucial the availability of high-quality data is for our ability to do so. Niehues and Peichl use gold-standard longitudinal data sets (the PSID for the US and the SOEP for Germany); and Hufe et al. use unusually rich cohort studies, as already mentioned. If we are to make similar progress elsewhere and, in particular, in the developing countries where our lower-bound estimates of IOp are much higher than in rich countries, then similarly rich data must be collected more widely.
Outcomes and opportunities: a circular flow
Should we see attempts to quantify IOp as substitutes for the measurement of income or wealth inequality? Certainly not! Inequality of opportunity and inequality of outcomes are intimately, causally, and circularly related. They are two sides of the same coin, and must be understood as such. Today’s outcomes – our own levels of education, income, and access to services, for example – are tomorrow’s circumstances – for our children. And today’s circumstances – differences in the quality of care children receive at home, or in the quality of the schools they attend, for example – clearly affect their outcomes tomorrow.
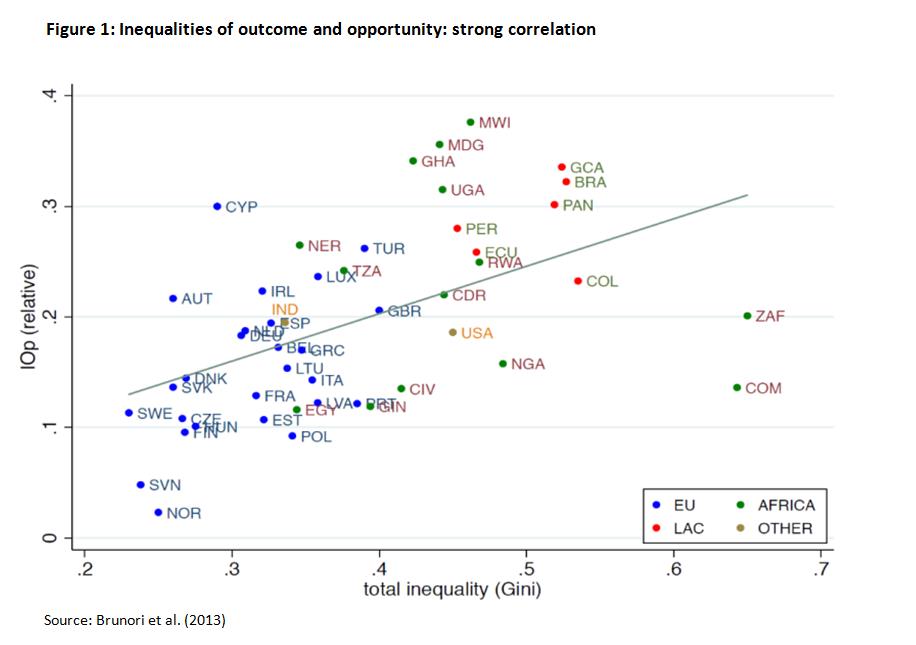
The positive, significant and substantial cross-country correlation between IOp (as a share of the total) and total income inequality that can be seen in Figure 1 reflects this circular causal flow between the distribution of opportunities and the distribution of outcomes. Indeed, although the pursuit of equality of opportunity does not imply a need to fully equalize incomes (as noted at the outset), their interdependence makes it unlikely that high levels of income or wealth inequality would be consistent with persistent, sustainable equality of opportunity.
Inequality of opportunity and outcome inequalities are complementary concepts, not substitutes. But the distinction matters. Behaviorally, there is some evidence that people are more averse to inequality of opportunities than to outcome inequalities arising from other sources (Cappelen et al., 2010). Consequentially, there is evidence (at least for the United States) that inequality of opportunities is more detrimental to subsequent economic performance than the residual component of inequality (Marrero and Rodriguez, 2013). And ethically, the balance of philosophical opinion is that opportunities, not outcomes, are the “currency of egalitarian justice” (Cohen, 1989). In all three domains, inequality of opportunity is, in a sense, the active ingredient of the inequalities we observe in society. It is the true enemy of egalitarians.
1 This short piece is loosely based on my lecture on “Inequality and Personal Responsibility”, at the European Investment Bank on 27 April 2017. I am grateful to Conchita d’Ambrosio and the University of Luxembourg for their hospitality, and to Daniele Checchi for encouraging me to write it up.
2 Taking “degrees of effort” to be given by the relative ranking of a person in his or her type is one way in which account can be taken of the effect of circumstances on absolute effort levels. See Roemer (1998).
References
| Barberà, S.; Bossert, W.; Pattanaik, P.K. (2004): “Ranking sets of objects”, in P. Hammond and C. Seidl (eds.), Handbook of Utility Theory, 2, Extensions. Kluwer. |
| Brunori, P.; Ferreira, F.H.G; Peragine, V. (2013): “Inequality of opportunity, income inequality and economic mobility: some international comparison”, Chapter 5 in E. Paus (ed.) Getting Development Right. New York, NY: Palgrave Macmillan. |
| Cappelen, A.; Sorensen, E.; Tungodden, B. (2010): “Responsibility for what? Fairness and individual responsibility”, European Economic Review 54: 429-441. |
| Cohen, G. A. (1989): “On the Currency of Egalitarian Justice”, Ethics 99: 906-944. |
| Ferreira, F. H. G. and Gignoux, J. (2011): “The Measurement of Inequality of Opportunity: Theory and an Application to Latin America”, Review of Income and Wealth, 57 (4): 622-657. |
| Ferreira, F. H. G. and Peragine, V. (2016): “Individual Responsibility and Equality of Opportunity”, Chapter 25 in M.D. Adler and M. Fleurbaey (eds.) Oxford Handbook of Well-Being and Public Policy. Oxford: Oxford University Press. |
| Hufe, P.; Peichl, A.; Roemer J.; Ungerer, M. (2015): “Inequality of Income Acquisition: The role of childhood circumstances”, ZEW Discussion Paper No. 15-084. |
| Marrero, G. and Rodríguez, J.G. (2013): “Inequality of opportunity and growth”, Journal of Development Economics 104: 107-122. |
| Niehues, J. and Peichl, A. (2014): “Upper bounds of inequality of opportunity: theory and evidence for Germany and the US”, Social Choice and Welfare 43 (1): 73-99. |
| Roemer, J. (1998): Equality of Opportunity. Cambridge, MA: Harvard University Press. |
| Sen, A. (1980): “Equality of what?” in S. McMurrin (ed.) The Tanner Lectures on Human Values. Salt Lake City: University of Utah Press. |
