
Issue, No.30 (June 2024)
Bridging Inequality of Opportunity, Sufficientarianism, and Limitarianism: A Framework for Assessing Unfair Inequality*
1. Introduction
Imagine that you are a policymaker and that one of your goals is to achieve a fair society. Given the complexity of what fairness might mean, one possible approach as a first step may be to use a measure of inequality of income distribution to compute how equitable society is.
The Gini index, for example, is one of the most widely used measures of inequality to obtain a numerical value of equity in the distribution of a country’s outcome. The Gini index varies between 0 (perfect equality) of outcomes and 1 (perfect inequality). A policymaker who cares about fairness will tend to prefer a distribution that generates values as close to 0 as possible. However, the index is 0 when all incomes are perfectly the same for all and equal to the mean. So, when we apply this index, it is as if we were comparing an empirical distribution of incomes to a hypothetical one where all incomes are equal. Should we then consider the latter as the normative reference distribution? Or, posed differently, should our society aspire to this distributional model? It seems logical to think that such a solution is rather extreme, even impossible to achieve. Yet every commonly implemented index of inequality, from Gini to measures of dispersion and entropy, assesses the goodness of income distribution with respect to its distance from a perfectly egalitarian distribution. In this paper, I propose one among the possible normative distributions that is much more feasible in practice than a perfectly egalitarian solution yet gathering relevant ethical considerations. Moreover, I will propose a measure of unfairness by computing how far the actual distribution appears from the ideal one.
A very recent work of Hufe, Kanbur, and Peichl (2022) has proposed a family of measures that incorporate the principles of equality of opportunity (EOp) and freedom from poverty (FfP). Overcoming prior studies which have tended to favor either EOp or FfP. (Brunori, Lugo, et al., 2013).
We start from that contribution to propose a simple way of measuring unfairness in a distribution of income embodying in co-equal fashion three normative principles: equality of opportunity, sufficientariansim, and limitarianism. We present the empirical estimation for Luxembourg, showing how much this country is not so far from the ideal distribution.
2. Social Norms in Brief
2.1 Equality of Opportunity
First, we want to build an ideal distribution that is satisfying equality of opportunity. It can be described as the social ethics, which seeks to level differences in outcomes, not attributable to individual responsibility, but not those for which individuals are responsible for. Following Roemer (1998), we distinguish between inequalities due to factors beyond the individual control and factors within their control, and we consider the inequalities due to the former as unfair (Ramos and Van de Gaer, 2012; Fleurbaey and Maniquet, 2011).
Moreover, the EOp ideal can be broken down into two ethical principles. The first principle of compensation asserts that society should compensate for differences in individual accomplishments due to circumstances. The second principle, the reward principle, requires not to compensate for differences in achievements due to responsibility (Checchi and Peragine, 2010).
Hence, we can define an EOp measure as an estimate of how far a given distribution of outcomes is from equal opportunity counterfactual distribution, in which differences in outcomes caused by circumstances have been compensated.
In concrete, this can be done, first, by dividing the population into types (τ): groups of individuals characterized by the same circumstances. To do that, we implement a machine learning approach (regression trees and forest). (Brunori, Ferreira, and Neidhofer, 2023)
Then, we re-scale each individual empirical income (χi), dividing it by the type-specific mean income (μτ)and multiplying it by the mean for the entire population (μχ). Thus, we get:
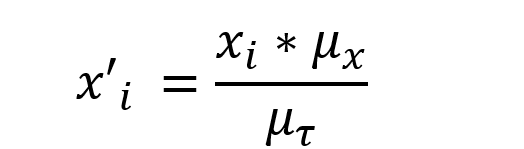
2.2 Sufficientarianism
Sufficientarianism is the second normative concern required in our work. It is an ethical doctrine recently analyzed axiomatically by Alcantud, Mariotti, and Veneziani (2022) and Bossert et al. (2022), but it traces back to Frankfurt’s thought (1987). In its original formulation, this principle assigns absolute priority to individuals below a certain threshold, and it cares only that everybody has enough.
Sufficientarianism raises questions about what constitutes “enough,” how it should be measured, and the implications for public policy. It often intersects with discussions on welfare and social justice, proposing a threshold-focused approach to resource distribution, which can lead to targeted interventions for those below the sufficiency threshold.
We satisfy this normative concern by applying a relative poverty line (θ), used to measure poverty based on the economic status of a population within a specific context. In particular, we implement a unique poverty line since we tend to believe that poverty is not a type-specific ethical concern. And we set it equal to 50% of the median of the entire distribution (as by OECD Statistics). Thus, our norm-based distribution, already equal in terms of opportunities, should not show any income below the poverty line: μχ ≥ θ
2.3 Limitarianism
According to the primary definition, Limitarianism, in his intrinsic view, is generally characterized by the claim that “it is not morally permissible to have more resources than are needed to flourish in life fully” (Robeyns, 2017)
However, we prefer to use the instrumental concept, as Limitarianism is necessary to realize“two intrinsic values: political equality … and the meeting of unmet urgent needs” (Robeyns, 2017)
Focusing on the urgent need argument, one possible “need” might be fighting poverty. Following this line, we have chosen to place the burden of defeating poverty on all those above an income threshold. Moreover, we built this threshold so that it corresponds to the level that ensures no poverty in each type. The idea is quite simple: we channel income from the rich to the poor, starting from the first richest person until his income drops to the level of the second richest individual, and then we take resources proportionally from the first and the second until they reach the income of the third or on until there are no poor, and so on. We make this procedure type-specific. Thus, we end with multiple and endogenously constructed richness lines (θτ). Here is a simple example of the mechanism we described:

For simplification, there is only one type, and Gτ is the total amount of resources that need to be taken from the rich.
3. Measuring Unfairness
3.1 Norm Distribution
Given all the conditions, we have been able to characterize the following norm-based distribution:
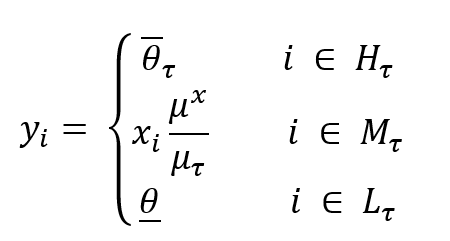
It is very simple to understand. The reference income yi should be equal to the richness lines (θτ) for all rich in each type. It should not be less than the common poverty line(θ) for the poor individual in each type and equal to the opportunity equalized income (xi μx/τx ) for the remaining individuals.
3.2 Divergence Measure
We implement a divergence measure of the empirical distribution from the norm-based one. This is not a novel approach. Distinguished works such as those by Cowell (1980), Magdalou and Nock (2011), and Almås et al. (2011) have broadened traditional approaches to quantifying inequality by means of divergences measures. The measure of divergence we choose is the one by Magdalou and Nock (2011):
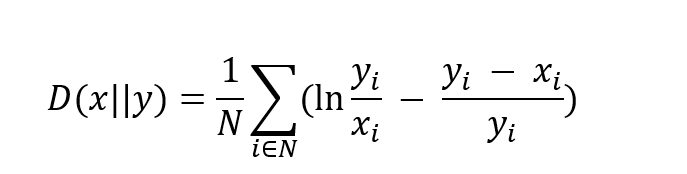
It is a simple measure of the discrepancy of the empirical individual distribution (xi) from the normative one (yi). The greater the discrepancy, the higher the measure and the stronger the unfairness in the distribution.
4. Empirical Application
4.1 Data
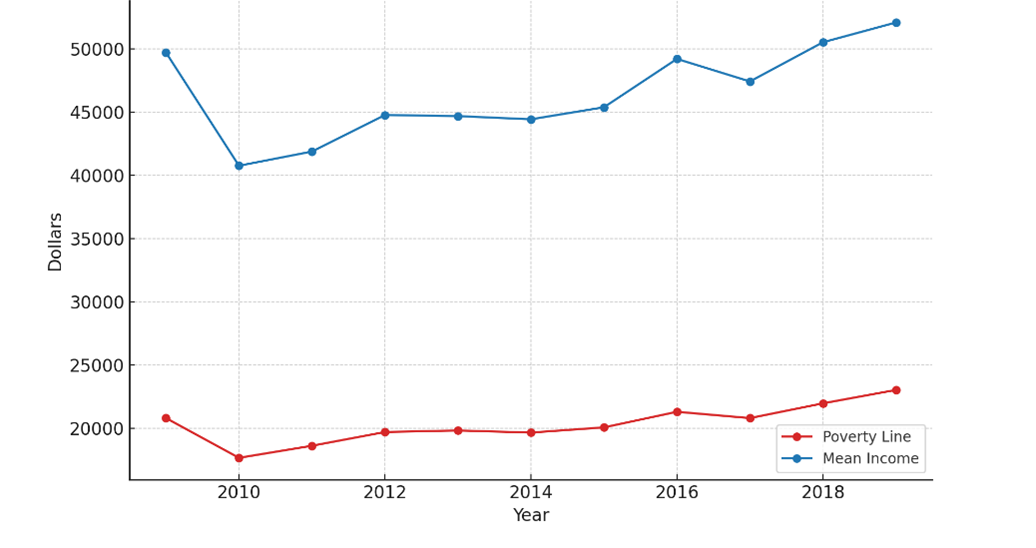
For the application, data from the LIS database for Luxembourg, covering the years 2009-2019, were used. The chosen outcome variable is the household equivalised disposable income, which has been adjusted using the consumer price index to 2019 values. The individual circumstances included are the father’s and mother’s education, gender, and birthplace. In Figure 1, we provide a simple representation by year of the average income and the poverty line levels.
Figure 1. Poverty line and mean income over years
4.2 Results
Figure 2 shows three different measurements of unfair inequality from 2009 to 2019.
The blue line represents the index of divergence computed with respect to a perfectly egalitarian distribution. In this specific situation, it corresponds to the standard Mean Logarithmic Deviation. The trend is stable, and the values, ranging from 0.16 to 0.13, show that Luxembourg’s distribution is relatively far from that of a totally egalitarian one.
Figure 2. Annual values of Dn, De, and Diop from 2009 to 2019
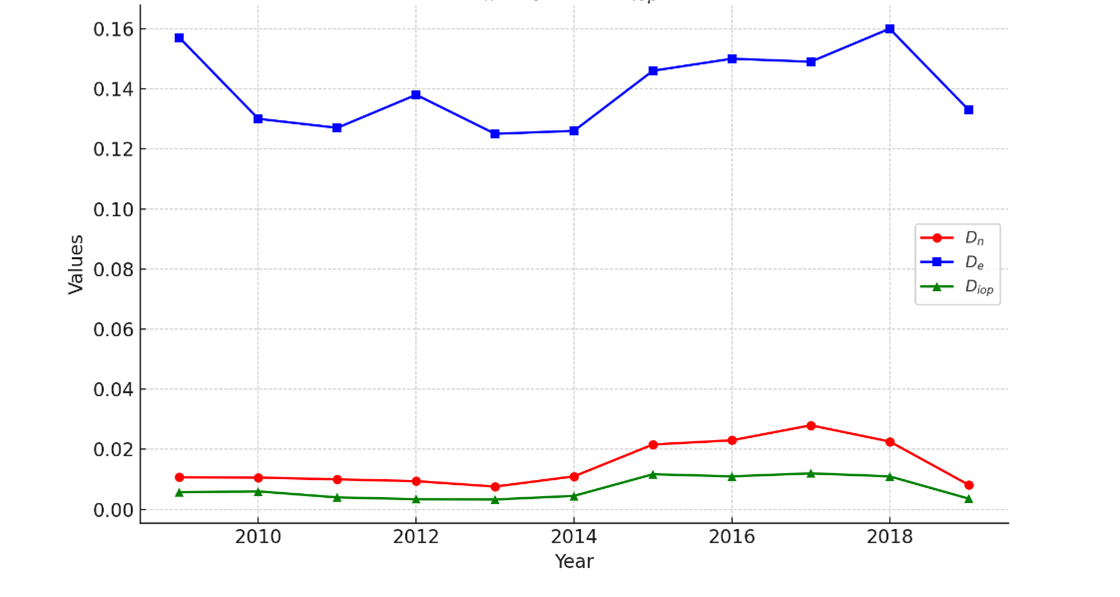
The red line represents the divergence compared with the norm-based distribution, which satisfies our three normative requirements. The values are relatively stable and much lower than the blue line, indicating less variation from the norm-based distribution compared to the perfectly egalitarian scenario.
The green line measures inequality of opportunity only. It shows the lowest values among the three indices, suggesting a relatively smaller contribution of opportunity inequality to the overall unfairness disparity.
5. Conclusion
We propose a characterization of a new norm-based distribution, which embodies three ethics: Equality of Opportunity, Sufficientarianims and Limitarianism. We measure the unfairness as a distance between the empirical distribution and the normative one.
The empirical application provides a clear visual representation of how different normative concerns can yield different insights into the nature and extent of inequality within a society. Inequality of opportunity alone is unable to explain the unfairness in Luxembourg’s income distribution (2009-2019) due to the fact that the actual distribution is close to the equal opportunity one. Moreover, the results show that the standard inequality index (blue line), measuring the distance of the distribution from the mean, is much larger than norm-based measures and, hence, far from a possible realization of reality. In addition, Luxembourg appears particularly close to the ideal distribution when both a threshold of poverty and multiple richness lines are included. This makes the normative distribution and its underlying principles a feasible realization and quite simple for a policymaker to implement.
* This article is an outcome of a research visit carried out in the context of the (LIS)2ER initiative which received funding from the Luxembourg Ministry of Higher Education and Research.
References
| Alcantud, J.C.R.; Mariotti, M.; Veneziani, R. (2022). “Sufficientarianism”. In: Theoretical Economics 17.4, pp. 1529–1557. |
| Almås, Ingvild; Cappelen, A.W.; Lind, J.T.; Sørensen, E. Ø.; Tungodden, B. (2011). “Measuring unfair (in)equality”. In: Journal of Public Economics 95.7-8, pp. 488–499. |
| Brunori, P., Ferreira, F.H.G, Neidhofer, G. (2023). Inequality of opportunity and intergenerational persistence in Latin America. Tech. rep. World Institute for Development Economic Research (UNU-WIDER). |
| Brunori, P.; Ferreira, F.; Lugo, M.A; Peragine, V. (2013). “Opportunity-sensitive poverty measurement”. In: World Bank Policy Research working paper 6728. |
| Checchi, D. and Peragine, V. (2010). “Inequality of opportunity in Italy”. In: The Journal of Economic Inequality 8, pp. 429–450. |
| Cowell, F. A. (1980). “Generalized entropy and the measurement of distributional change”. In: European Economic Review 13.1, pp. 147–159. |
| Cowell, F. A. (1985). “Measures of distributional change: An axiomatic approach”. In: The Review of Economic Studies 52.1, pp. 135–151. |
| Fleurbaey, M. and Maniquet, F. (2011). A theory of fairness and social welfare. Vol. 48. Cambridge University Press. |
| Frankfurt, Harry (1987). “Equality as a moral ideal”. In: Ethics 98.1, pp. 21–43. |
| Hufe, P.; Kanbur, R.; Peichl, A. (2022). “Measuring unfair inequality: Reconciling equality of opportunity and freedom from poverty”. In: The Review of Economic Studies 89.6, pp. 3345–3380. |
| Magdalou, B. and Nock, R. (2011). “Income distributions and decomposable divergence measures”. In: Journal of Economic Theory 146.6, pp. 2440–2454.8. |
| Ramos, X. and Van de Gaer, D. (2012). “Empirical approaches to inequality of opportunity: Principles, measures, and evidence”. In: Journal of Economic Surveys, 30(5), 855-883. |
| Robeyns, I. (2017). “Having too much”. In: Nomos 58, pp. 1–44. |
| Roemer, J.E. (1998). Equality of opportunity, Harvard University Press, Cambridge. |
